Polytope
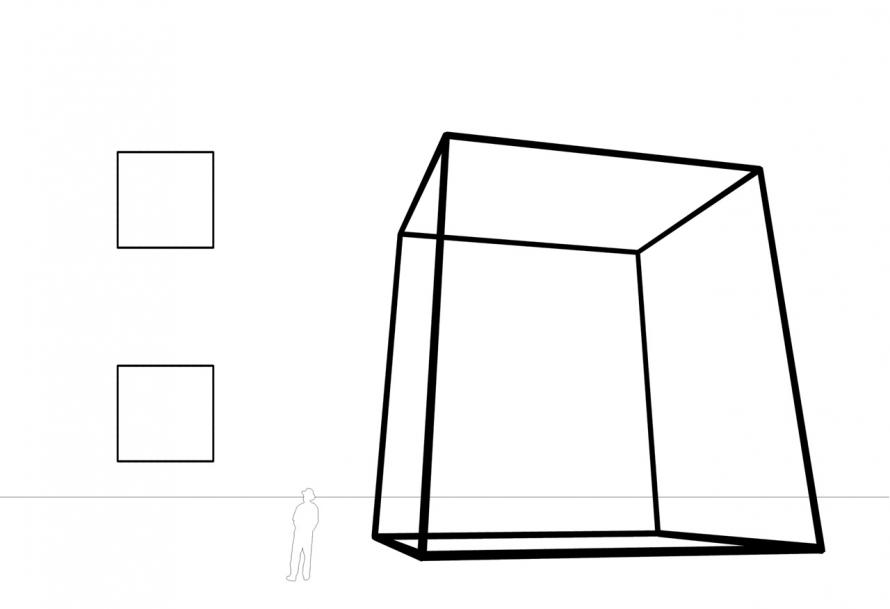
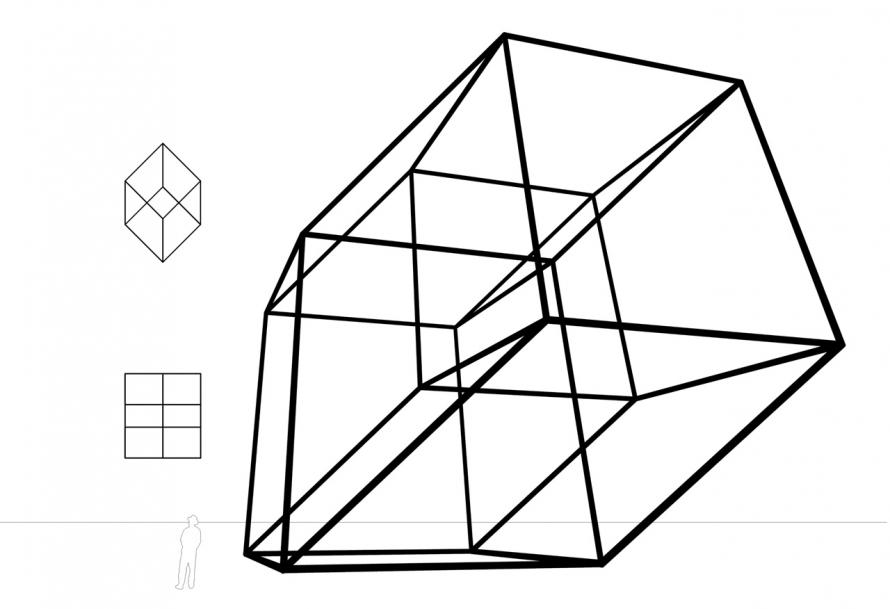
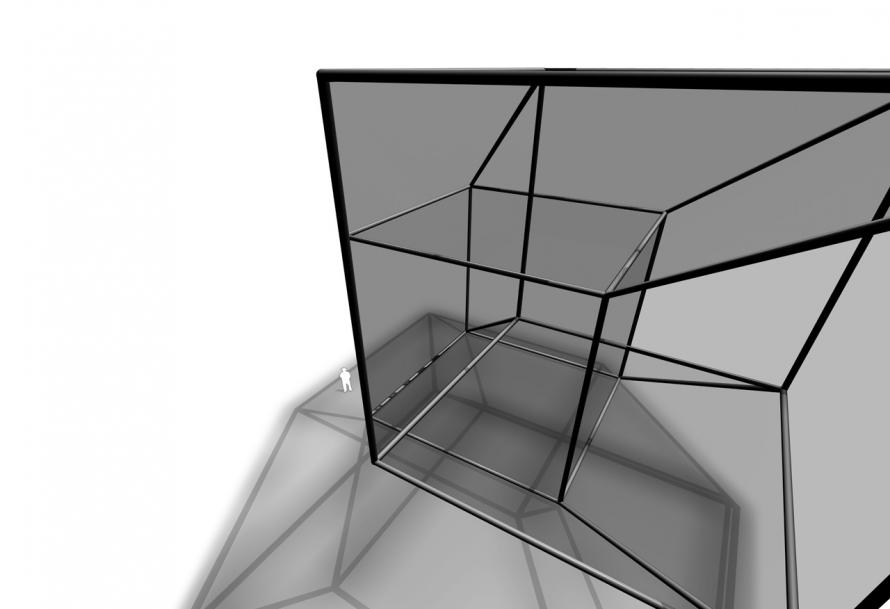
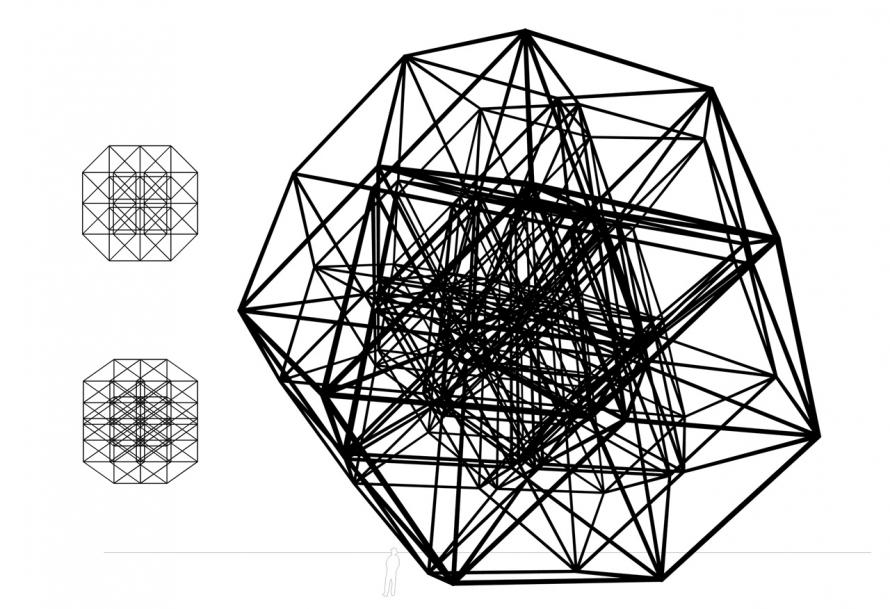
Die Mathematiker Gauß und Riemann untersuchten im 19.Jh mehrdimensionale räumliche Gebilde und diskutierten über die Frage, ob es einen 4-dimensionalen Raum gibt in dem sich ein 4-dimensionaler Würfel unverzerrt darstellen läßt. In seinem Roman Flatland (A Romance In Many Dimensions) thematisierte Edwin A. Abbott (1838-1926) diese Relativität der Wirklichkeit. Er beschreibt eine Flächenwelt und den Versuch eines 3-dimensionalen Körpers (einer Kugel) einem Flächenwesen (einem unregelmäßigen Sechseck) die dritte Dimension zu erklären. Mithilfe einer mathematischen Reihe, die von einem Punkt aufsteigend bis zum 3-dimensionalen Würfel die Zahl der Punkte, Strecken, Flächen angibt, die das nächst höherdimensionale Polytop beschreiben, versucht die Kugel dem Sechseck begreifbar zu machen, was die dritte räumiche Dimension sei. Damit wirft sie gleichzeitig die Frage auf, ob eine vierte, fünfte... räumliche Dimension existiert, die mittels der gleichen Reihe beschrieben werden kann.
Die Faszination 3-dimensionaler Darstellungen n-dimensionaler Orthogone erschließt sich bei näherer Auseinandersetzung mit diesen Objekten. Man beginnt komplexe und eigenwillige Strukturen zu entdecken. Schiefe Würfel, unbekannte Körper... Der Gedanke daran, daß es »wirklich« eine vierte, fünfte, sechste... räumliche Dimension gibt scheint weniger abstrakt und umso geheimnisvoller, wenn man nicht mathematische Reihen, Formeln sondern konkrete Gebilde vor sich hat.
Studie
Moritsch, 2005